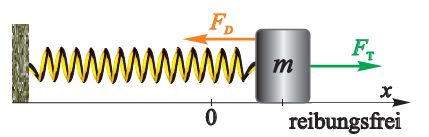
Federpendel
Physikalisch treten Schwingungen auf, wenn es in einem System zu einem periodischer Wechsel zweier Energieformen kommt. Dabei ist eine Energie potenzieller, die andere kinetischer Natur. Solche schwingungsfähigen Systeme sind z.B. verschiedene Pendel oder Schwingkreise. Man nennt sie auch Oszillatoren. Von besonderer Bedeutung sind harmonische Schwingungen, die als Sinusfunktion dargestellt werden können.
Mathematisch erhält man eine Schwingungsfunktion aus einer Differenzialgleichung 2. Ordnung. Im Fall einer harmonischen Schwingung eines Oszillators lautet diese \(\ddot x+ω^2 \cdot x = 0\). Dabei ist \(x\) die sich periodisch ändernde Kenngröße, z.B. Weg, Drehwinkel, Auslenkung, Spannung, Stromstärke. \(\ddot x\) die zweite Ableitung dieser Größe nach der Zeit. Ableitungen nach der Zeit \(t\) werden oft mit Punkten über dem Größensymbol angegeben und nicht mit dem sonst üblichen Strich.
Allgemeine Sinusfunktion
Abhängig von Parametern lautet die allgemeine Sinusfunktion \(x(t) = r\cdot\sin(ω\cdot t+φ)\).
- \(x\) … Auslenkung bzw. Abstand von der Ruhelage
- \(t\) … Zeit
- \(r\) … Amplitude
- \(f\) … Frequenz in Hz (Anzahl der periodischen Vorgänge pro Sekunde)
- \(ω=2πf\) … Kreisfrequenz
- \(T=\frac{1}{f}\) … Periodendauer (kürzester Zeitabschnitt zwischen zwei gleichen Zuständen des Oszillators)
- \(φ\) … Phasenlage in rad, sie wird manchmal auch im Altgrad angegeben und ist dann ins Bogenmaß umzurechnen.
Darstellung mit einer Tabellenkalkulation
Als Anleitung sollte der Screenshot und die Erklärung für die Darstellung von Funktionen
ausreichend sein. Im Folgenden sind nur einige Besonderheiten aufgeführt.

Darstellung einer Schwingungsfunktion
| Zelle | Inhalt |
| E5 | Hier erfolgt die Eingabe der Frequenz in Hz. |
| E6 | Berechnung der Kreisfrequenz: =2*PI()*E5 |
| E7 | Eingabe der Phasenlage soll in rad erfolgen. |
| A5 | übernimmt des Startwert des Intervalls aus E8: =E8 |
| A6 | Das Intervall wird in 50 Teile aufgeteilt: =A5+(E$9-E$8)/50 nach unten ausfüllen bis A55. |
| B5 | Formel: =E$4*SIN(E$6*A5+E$7) nach unten ausfüllen bis B55. |
Abschließend markiert man die Wertetabelle und startet den Diagrammassistenten. Dort wählt man das PunktXY-Diagramm als Typ aus.
Weitere Aufgaben
- Die Funktionalität kann noch mit Schiebereglern für die einzelnen Parameter verbessert werden.
- Darstellung einer gedämpften Schwingung: \(x=r\cdot e^{-δ\cdot t}\cdot \sin(ω\cdot t+φ)\) mit dem zusätzlichen Parameter \(δ\) für die Dämpfung.
- Von besonderem Interesse ist auch die Überlagerung zweier Schwingungen. Dafür wird eine weitere \(x\)-Spalte für die zweite Schwingung mit eigenen Parametern und eine Spalte für die Summe der beiden Schwingungen hinzugefügt. Dargestellt wird nur die Summenschwingung.
- Jede beliebige Schwingung kann als Summe von harmonischen Schwingungen dargestellt werden. Das Ergebnis ist dann eine Fourierreihe.
- Die Überlagerung zweier Schwingungen mit mit normal aufeinander stehenden Schwingungsrichtungen nennt man Lissajousfigur.
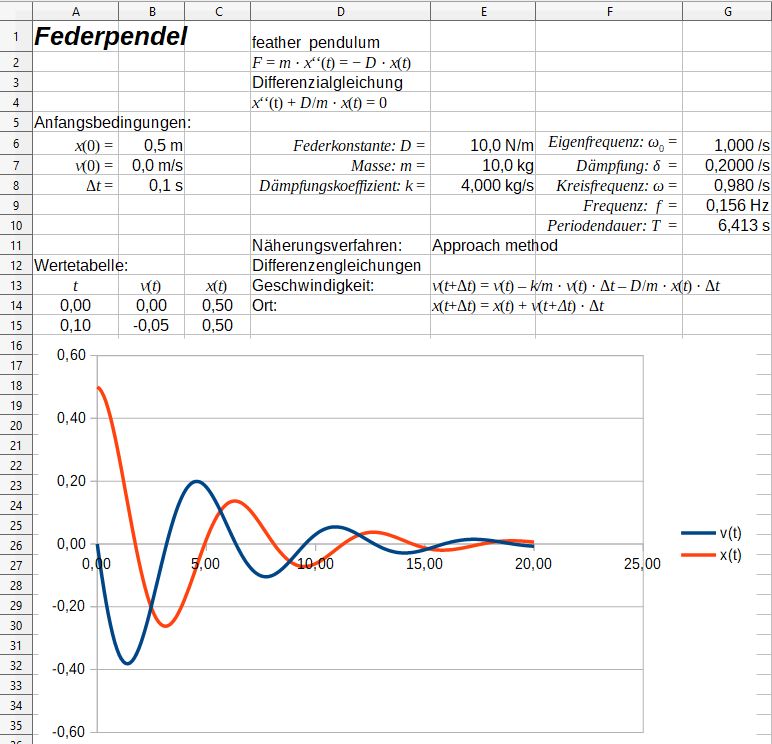
Differenzengleichung für das gedämpfte Federpendel

Überlagerung zweier Schwingungen

Überlagerung dreier Schwingungen

Lissajous-Figur

Fourierreihen
Inhalte:
- absolute und relative Zellbezüge
- automatisches Ausfüllen
- xy-Diagramm
