Bei einer Epidemie breitet sich eine Krankheit in einer Population von Individuen aus. Mit einer Tabellenkalkulation kann man einfache Modelle für den Verlauf von Epidemien umsetzen. Dazu sind im Prinzip nur die Grundrechnungsarten erforderlich.
Bei einer Epidemie gibt es erkrankte und gesunde Individuen, die man Klassen nennt. Verläuft die Krankheit auch tödlich, so ergibt sich eine weitere Klasse der Toten. Bei Epidemiemodellen beobachtet man den zeitlichen Verlauf der Anzahl von Gesunden, Kranken und Toten (Mehrklassenmodelle). Bei Wachstumsmodellen hat man meistens nur eine Klasse.
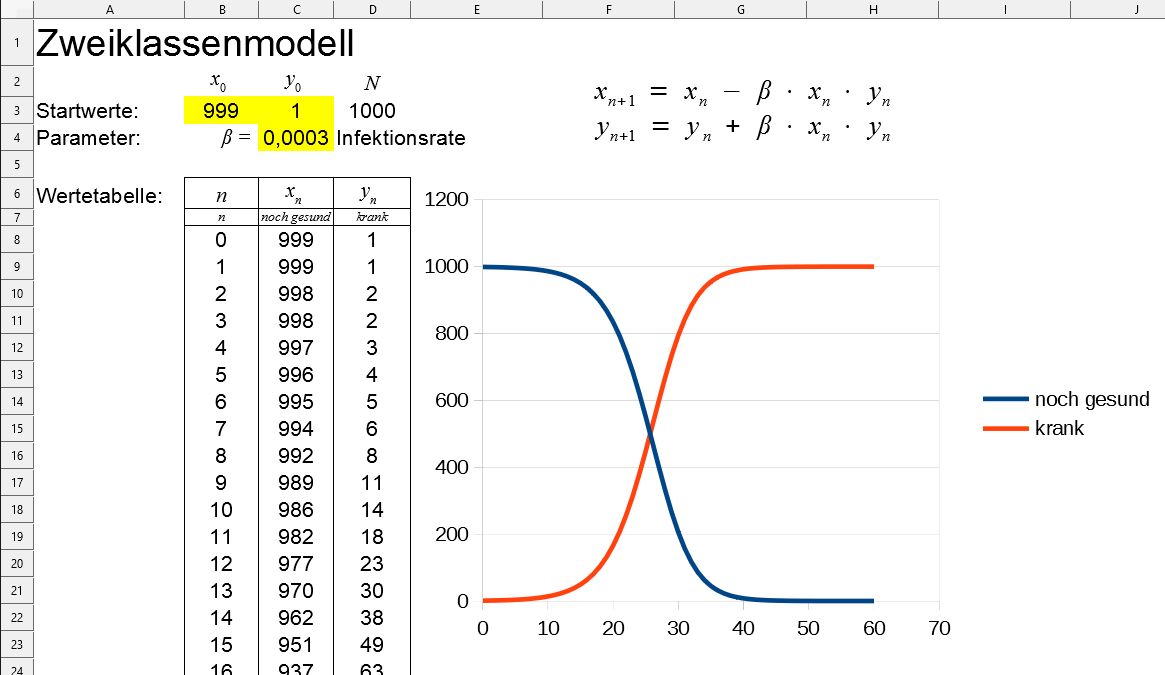
Zweiklassenmodell mit Infektion
Bei unserem ersten Beispiel einer Epidemie (z. B. Grippewelle) werden die Individuen einer Population durch ihren Gesundheitszustand unterschieden: gesund und krank. Daraus ergeben sich die beiden Beobachtungsgrößen (Klassen):
- \(x_k\) … Anzahl der Gesunden zum Zeitpunkt \(t_k\)
- \(y_k\) … Anzahl der Kranken zum Zeitpunkt \(t_k\)
Die Population sei abgeschlossen, d. h. zu jedem Zeitpunkt ist \(x_k+y_k=N=\text{konst.}\)
Damit man den Verlauf einer Epidemie modellieren kann, ist es wichtig, alle Parameter zu kennen, die die Verbreitung einer Krankheit kennzeichnen. Einer dieser Parameter ist die Infektionsrate. Sie legt fest, wie eine Krankheit von einem Kranken auf einen Gesunden übertragen wird. In einem ersten Schritt werden wir nur mit einer über den gesamten Beobachtungszeitraum konstanten Infektionsrate \(β\) rechnen. Dann erhält man das System von Differenzengleichungen:
\(x_{k+1} = x_k − β \cdot x_k\cdot y_k\)
\(y_{k+1} = y_k + β \cdot x_k\cdot y_k\)
Die Infektionsrate \(β\) kann empirisch bestimmt werden.
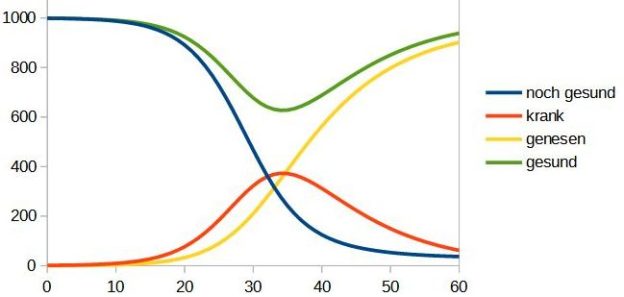
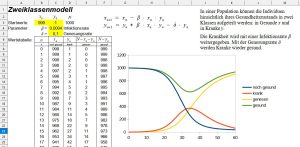
Zweiklassenmodell mit Infektion und Genesung
Im nächsten Schritt wird das Genesen der Kranken mit einem Parameter \(\delta\) (Genesungsfaktor) berücksichtigt:
\(x_{k+1} = x_k − β \cdot x_k\cdot y_k\)
\(y_{k+1} = y_k + β \cdot x_k\cdot y_k-\delta\cdot y_k\)
Genesene können nicht mehr erkranken, sie sind immun. Die Anzahl der genesenen Individuen ist dann \(N-x_k-y_k\). Insgesamt sind Individuen \(N-y_k\) gesund. Die Tabelle, die oben beschrieben wird, kann einfach entsprechend angepasst und um entsprechende Spalten ergänzt werden.
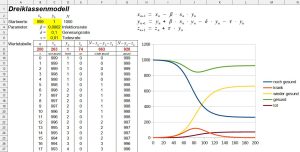
Dreiklassenmodell mit Infektion und Sterben
Kann eine Krankheit auch tödlich verlaufen, wird das Modell um eine dritte Klasse \(z_k\) (Anzahl der Toten zum Zeitpunkt \(t_k\)) ergänzt. Die Sterberate \(\gamma\) wirkt nur auf die Klasse der Kranken:
\(x_{k+1} = x_k − β \cdot x_k\cdot y_k\)
\(y_{k+1} = y_k + β \cdot x_k\cdot y_k-\gamma\cdot y_k\)
\(z_{k+1} = z_k + \gamma\cdot y_k\)
Dreiklassenmodell mit Infektion, Sterben und Genesung
\(x_{k+1} = x_k − β \cdot x_k\cdot y_k\)
\(y_{k+1} = y_k + β \cdot x_k\cdot y_k-\delta\cdot y_k-\gamma\cdot y_k\)
\(z_{k+1} = z_k + \delta\cdot y_k\)
In weiteren Schritten kann das Modell angepasst werden, indem man Geburtenrate, natürliche Sterberate, Infektionswege (Kontaktnachverfolgung), Inkubationszeit sowie Migration zwischen Habitaten (Wanderungen bzw. Reisetätigkeit) berücksichtigt.