Bei dynamischen Prozessen werden zeitliche Veränderung von Größen beobachtet. Bei der Modellierung entwickelt man oft Differenzialgleichungen. Mit der Tabellenkalkulation hat man die Möglichkeit mit einfacheren Differenzengleichungen durchaus komplexe Zusammenhänge darzustellen. Differenzengleichungen sind Gleichungen der Form \(x_{n+1} = f(x_n)\) mit einem bestimmten Anfangswert \(x_0\) . Der Index \(n\) ist eine natürliche Zahl, die jeweils gleichen Zeitabschnitten entspricht: z.B. \(n=0\) bezeichnet den Ausgangswert, \(n=1\) nach dem ersten Tag, \(n=2\) nach dem zweiten Tag usw.
Wachstumsmodelle
Unter Wachstum versteht man allgemein einen zeitlichen Prozess, bei dem die Gesamtmasse bzw. Gesamtmenge einer Struktur (z. B. Zelle, Gewebe, Organismus, Material, Population) zunimmt.
Lineares Wachstum
In gleichen Zeitabschnitten nimmt die beobachtete Größe \(x\) jeweils um einen konstanten Betrag \(b\) zu:
\(x_{n+1}=x_n+b\)
Anleitung für die Tabellenkalkulation:
| Zelle | Inhalt |  |
| A1 | Überschrift: Lineares Wachstum |
|
| A3 | Text: Startwert: |
|
| B3 | Text: x0 = |
|
| C3 | Eingabefeld für den Startwert \(x_0\) | |
| A4 | Text: Parameter: |
|
| B4 | Text: b = |
|
| C4 | Eingabefeld für den Parameter \(b\) | |
| A6 | Text Wertetabelle |
|
| B6 | Spaltenüberschrift n |
|
| B7 | Eingabe 0 -> nach unten ausfüllen bis 14 |
|
| C6 | Spaltenüberschrift x0 |
|
| C7 | Startwert übernehmen: =C3 |
|
| C8 | Formel: =C7+$C$4für die Berechnung der Funktionswerte -> nach unten ausfüllen |
|
Eingabefelder sind gelb unterlegt. Nun markiert man die Wertetabelle und startet den Diagrammassistenten. Dort wählt man das xy-Diagramm als Typ aus.
Das Filmchen zeigt Schritt für Schritt den Aufbau der Tabelle in LibreOffice Calc.
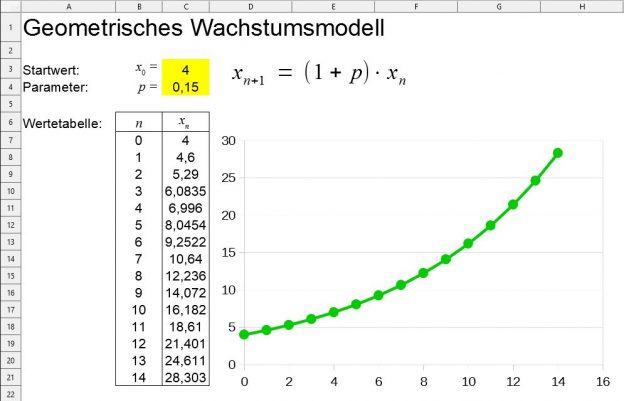
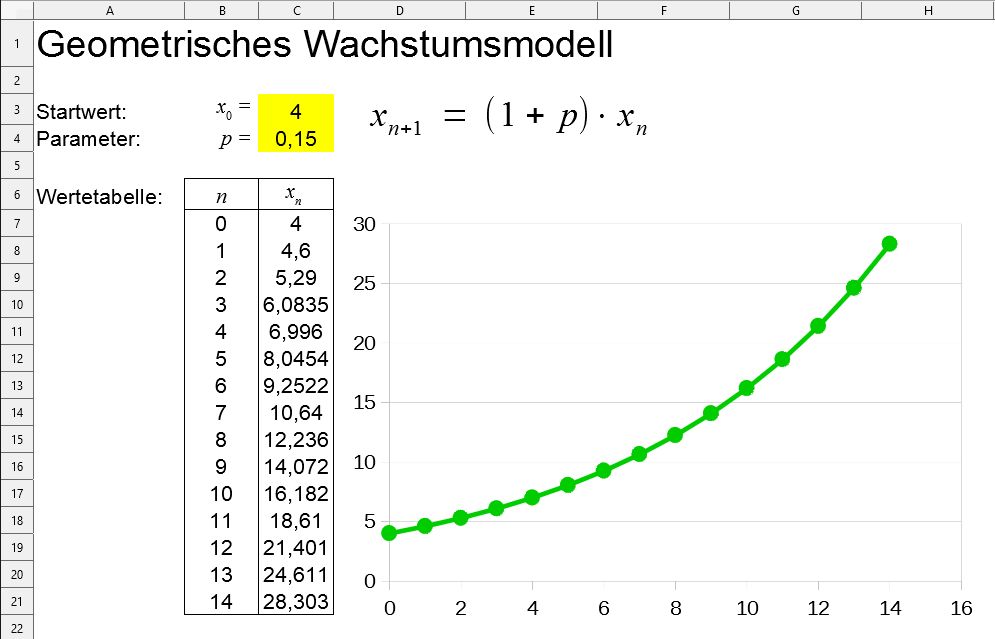Geometrisches bzw. exponentielles Wachstum
Beim geometrischen bzw. exponentiellen Wachstum vervielfacht sich der Wert der Beobachtungsgröße \(x\)in gleichen Zeitabschnitten. Es wird der vorhergehnde Wert der Größe mit einer konstanten Zahl \(a\) multipliziert:
\(x_{n+1} = a\cdot x_n\)
Oft wird die Zunahme in Prozent ausgedrückt und man schreibt dann
\(x_{n+1} = (1+p)\cdot x_n\)
mit dem Prozentsatz \(p\). Ist \(p<0\), so nimmt die Beobachtungsgröße ab.
Beispiele für exponentielle Verläufe sind z. B. Bakterienwachstum, radioaktiver Zerfall, Temperaturabkühlung, aber auch der Zinseszins. Ein entsprechendes Arbeitsblatt ist mit der Vorlage des vorigen Beispiels leicht umzusetzen. Testen Sie auch die Auswirkungen auf den Verlauf für Prozentsätze \(0>p>-1\) für \(p<-1\) .
Kombination von geometrischem und linearem Wachstum
Mit einer Differenzengleichung 1. Ordnung \(x_{n+1} = a\cdot x_n + b\) können zum Beispiel Fragestellungen wie diese dargestellt werden:
Beim Rauchen wird dem Körper eine gewisse Menge an schädlichem Nikotin (z. B. 0,02 mg täglich) zugeführt. Durch biochemische Prozesse wird dieses Nikotin im Blut wieder abgebaut und ausgeschieden (z. B. 1 % täglich). Wie entwickelt sich der Nikotingehalt, wenn er zu Beginn der Beobachtung Null ist?
Für verschiedene Kombinationen der Parameter \(a\) und \(b\) ergeben sich folgende Verläufe:
Die Funktionalität kann noch mit Bildlaufleisten (Schieberegler) für die einzelnen Parameter
verbessert werden.
Inhalte:
- absolute und relative Zellbezüge
- automatisches Ausfüllen
- xy-Diagramm
- Rekursion